Zum Inhaltsverzeichnis
Zurück zu Kapitel 3

4. Das Fitverfahren

Die folgende Beschreibung des Fitverfahrens zur Impulsbestimmung ist eine Zusammenfassung der wichtigsten Ergebnisse aus der Diplomarbeit von Claus Dohmen [Do 91].

Von einem aus dem Target kommenden Teilchen soll der Impuls beim Eintritt in die Driftkammer DC1 bestimmt werden. Dazu wird die Spur des Teilchens mit Hilfe eines c² - Fits iterativ unter Verwendung eines Spurmodells an die in den Driftkammern DC1 und DC2 bestimmten Koordinaten angepaßt. Die Inhomogenität des Magnetfeldes wird dabei voll mitberücksichtigt. Da die Messungen der Spurpunkte in den beiden Kammern unterschiedliche Genauigkeiten haben, müssen die Meßpunkte mit unterschiedlichem Gewicht in den Fit eingehen. Nicht berücksichtigt im Fitprozeß werden
jedoch Vielfachstreuung und Energieverlust, die nicht einfach zu behandeln sind und bei vielen Ereignissen keine große Veränderung des Fitergebnisses bedingen. In meiner Arbeit werden jedoch auch diese Vernachlässigungen mitbehandelt, was in späteren Kapiteln beschrieben wird.

4.1 Flugbahn eines Elektrons im SINDRUM II-Detektor

Die gesuchten Elektronen sind im Target entstanden und haben einen Impuls von etwa 100 MeV/c. Bei homogenem Magnetfeld, ohne Vielfachstreuung und Energieverlust, wäre die Bahn des Elektrons genau eine Helix. Es gibt zwei Typen von Spurverläufen (s. Abb. 4.1). Wenn der Transversalimpuls groß genug ist, gibt es pro Umlauf zwei Spurstücke in der DC1 und eines in der DC2. Ist der Transversalimpuls kleiner, so gibt es nur ein zusammenhängendes Spurstück in der DC1. Nach einem vollen Umlauf kann das Elektron die DC1 wieder erreichen. Da das Elektron laufend Energie verliert, ist i.a. der erste Spurkreis deutlich größer als die folgenden.
Da das Magnetfeld nicht ganz homogen ist und keine geschlossene Lösung der Bewegungsgleichung für dieses B-Feld bekannt ist, wird die Spur aus vielen hinreichend kleinen Helixstücken zusammengesetzt, so daß das B-Feld im Bereich eines Stückes als konstant angenommen werden kann [Si 14]. An den Übergangsstellen muß Impulserhaltung gelten. Durch diese Bedingung folgt ein stetiger differenzierbarer Übergang von einem Helixstück zum nächsten. In der x/y-Ebene können zwei Kreissegmente, auch mit unterschiedlichem Radius, stetig differenzierbar aneinandergesetzt werden. In der Bogen - z-Darstellung ist eine Helix allerdings eine Gerade, und zwei Geraden unterschiedlicher Steigung bilden am Ansatzpunkt einen Knickpunkt. Um dieses Problem zu lösen, wird z für die Spurfortsetzung als Funktion zweiten Grades von b angesetzt. Es reicht also, die Parameter des ersten Helixstückes bei Eintritt des Teilchens in die DC1 (bei Punkt A in Abb. 4.1) anzugeben, um die gesamte Spur zu beschreiben. Eine Helix wird durch sechs Parameter charakterisiert. Da der Punkt A immer auf der DC1-Innenwand liegt, genügen fünf Parameter (s. Abb. 4.2). Bei einer Projektion der Helix in die x/y-Ebene erhält man einen Kreis, den man durch Mittelpunkt (x_M,y_M) und Radius (R) beschreiben kann. Ein weiterer Parameter ist die z-Koordinate ß des Punktes A. Wenn man den z-Vorschub durch den Bogen (b) teilt, erhält man den fünften Parameter (a=D_z/D_b). Eine andere Beschreibung des Parameters a ist a = P_Z/P_T, also das Verhältnis von z-Impuls zu Transversalimpuls ( in der x/y-Ebene).

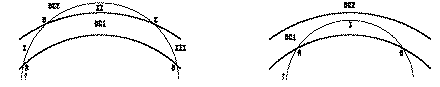
(a) (b)

Abb. 4.1. Die beiden für einen Fit brauchbaren Spurverläufe im SINDRUM II-Detektor. Bei großem Transversalimpuls erreichen die Elektronen die DC2 (a), bei kleinerem bleiben sie in der DC1 (b). Die Durchstoßpunkte durch die Kammerwände sind mit A bis D gekennzeichnet, die Spurbereiche mit I bis III.

(a) (b)

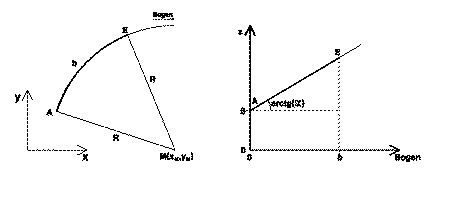
Abb. 4.2. Bedeutung der fünf Helixparameter in der x/y-Ebene (a) und im b/z-Diagramm (b). A ist der Anfangspunkt des Helixstückes. Beim ersten Helixstück ist es der Spurpunkt A. E ist der Endpunkt des Helix

stückes.

4.2 Hits im SINDRUM II-Detektor

In den beiden Kammern DC1 und DC2 liefert die Zeitinformation der Pulse auf den Anodendrähten eine Information zur x- und y-Koordinate. Man erhält allerdings nicht einen Punkt, sondern eine Isochrone . In der DC1 hat diese Isochrone Halbkreisform. Da in der DC2 der Isochronenradius eine kompliziertere Form hat und der Meßfehler bedeutend größer als in der DC1 ist, kann hier in erster Näherung die Isochrone als Punkt angenommen werden. In der DC1 liefern die Kathodenstreifen zusätzlich eine z-Koordinate. Diese Aufteilung in einerseits x- und y-Koordinaten und andererseits z-Koordinaten spiegelt sich auch im Fit wieder. Formell werden die Hits in Anodenhits und Kathodenhits aufgeteilt. Dies ist vor allem sinnvoll, da nicht zu jedem Anodenhit ein Kathodenhit existiert. Ein anderer Grund für diese Aufteilung ist der, daß der Meßfehler in z größer ist als in x/y, die z-Information also mit einem geringeren Gewicht in den Fit eingehen muß.

4.3 Abstände der Hits zur gefitteten Spur

4.3.1 Anodenhits

Da die Anodenhits nur als Isochrone bekannt sind und die Projektion der gefitteten Spur in die x/y-Ebene einen Kreis bildet, läßt sich kein eindeutiger Abstand zwischen Hit und gefitteter Spur angeben. Nimmt man aber an, daß die wirkliche Spur die Isochrone nur in einem Punkt berührt (s.o.) und dort etwa parallel zur gefitteten Spur verläuft, so wird dadurch ein Punkt auf der Isochrone ausgezeichnet. Der Abstand dieses Isochronenpunktes zur gefitteten Spur ist gleich dem Abstand entlang der Geraden, die durch den Isochronenmittelpunkt ( M_I) und den Spurmittelpunkt (M_S) geht (s. Abb. 4.3). Der Abstand ergibt sich also zu:

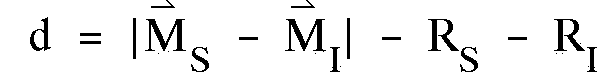(4.1)
Die beiden Vektoren M_S und M_I sind zweidimensional. R_S ist der Spurkreisradius und R_I der Isochronenradius.

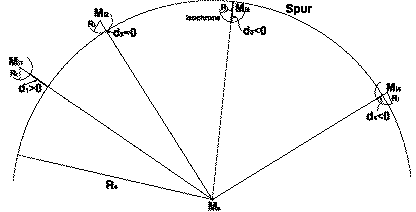
Abb. 4.3. Bestimmung des Abstandes eines DC1-Anodenhits zur gefitteten Spur. Eingetragen sind die Spur mit Mittelpunkt M_S und vier Hits mit ihren Isochronen. Die Abstände d_i sind dicker eingezeichnet. Die Projektion der Spur ist als einfacher Kreis angenommen.

Als Hitpunkt wird also der Isochronenpunkt gewählt, der sich am nächsten zum Spurkreismittelpunkt befindet. Der Spurpunkt ist der diesem am nächsten gelegene Punkt auf der gefitteten Spur. Befindet sich dieser Hitpunkt innerhalb des Spurkreises, so ist d negativ, sonst positiv.

4.3.2 Kathodenhits

Da nur Kathodenhits benutzt werden können, zu denen ein Anodenhit gefunden wurde, liegen hier alle drei Koordinaten vor. Als Hitpunkt wird wieder der im vorigen Abschnitt bestimmte benutzt. Der (z-)Abstand des Kathodenhits zur Spur ergibt sich dann zu:

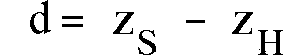(4.2)
Dabei ist z_S die z-Koordinate des Spurpunktes und z_H die des Hitpunktes.

4.4 Minimierung der Abstände der Hits zur Spur

Der Fit besteht aus einer iterativen Anpassung der fünf Spurparameter an die vorhandenen Hits. Ausgehend von einer groben Näherung der Spur wird wiederholt berechnet, wie die Spurparameter geändert werden müssen, um die Abstände der Hits zur gefitteten Spur zu minimieren. Dabei müssen die Abstände unterschiedlich gewichtet werden. Als einfachsten Gewichtungsfaktor kann man das Inverse des Meßfehlers (s.Tab. 3.1) nehmen. Man erhält dann:

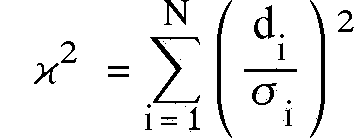(4.3)
Dieser Ansatz ist nur dann richtig, wenn die Fehler der einzelnen Hits unabhängig von einander sind. Da dies nicht unbedingt der Fall ist, bietet sich eine andere Schreibweise an, die einfacher auf abhängige Fehler zu verallgemeinern ist:

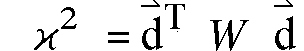(4.4)
Der Vektor d beinhaltet alle Hitabstände d_i . Die Matrix W ist die Gewichtsmatrix; im Falle unabhängiger Meßfehler ist sie diagonal und ihre Elemente sind:

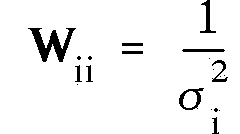(4.5)
Die fünf Parameter (x_M, y_M, R, a und ß) werden zu einem Vektor P zusammengefaßt. In jeder Iterationsstufe des Fits werden Korrekturen ( p ) zu P berechnet, um c² zu minimieren.

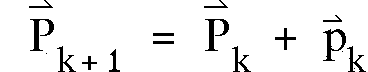(4.6)
Der Index k gibt die Iterationsstufe des Fits an.
Die Abstände der Hits hängen von den Spurparametern (P) ab. Berechnet man die 1. Ableitung D_ij der Abstände nach der Änderung (p) der Spurparameter, so läßt sich in 1. Näherung der Abstandsvektor der korrigierten Spur berechnen:

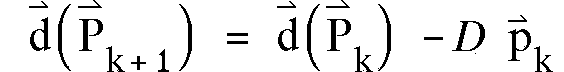(4.7)

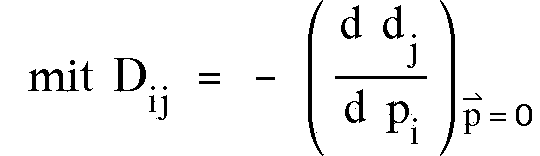            (4.8)
d(P_k) wird direkt aus der unkorrigierten Spur bestimmt. Um D_ij zu erhalten, wird beim Berechnen der Spur zu jeder Größe auch ihre 1. Ableitung nach den Spurparametern berechnet.
Damit läßt sich dann auch c²(P_k+1) berechnen, man erhält:
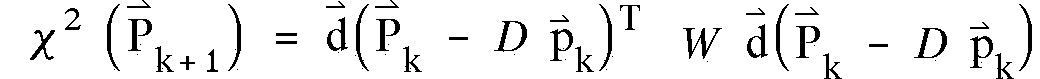    (4.9)
Die Minimierungsbedingung lautet:
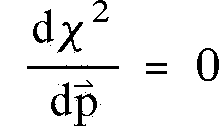                                                                                                              (4.10)
Aus den beiden letzten Gleichungen läßt sich p berechnen und ergibt sich zu:
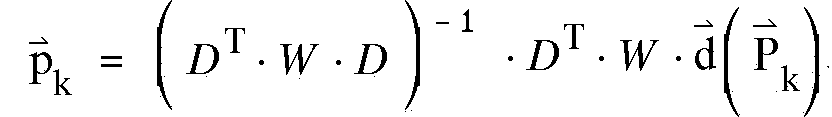                          (4.11)
Man erhält so nach (4.1) die Spurparameter der nächsten Iterationsstufe. Als Spur in der ersten Iterationsstufe nimmt man eine Helix, die man aus einem einfachen Kreisfit in x/y und einer linearen Anpassung in z erhält. Da die Korrekturen i.a. aber nur eine Näherung 1. Grades darstellen, ist das Resultat noch nicht die gesuchte Spur, sondern nur eine bessere Näherung. Wie bereits erwähnt, wird deshalb dieser Prozeß wiederholt, bis das Ergebnis gut genug ist. Hier haben sich drei Durchläufe als ausreichend gezeigt [Do 91].

4.5 Bestimmung der Gewichtsmatrix und Fehlerrechnung

Die Meßfehler der Hits sind voneinander unabhängig. Also würde für die Gewichtsmatrix eigentlich der Ansatz nach (4.5) ausreichen. Für die Berechnung von p ist aber nicht der Ort eines Hits wichtig, sondern sein Abstand zur gefitteten Spur. Hier geht also auch der Fehler der Spurrekonstruktion ein. Außer den sehr kleinen systematischen Fehler des Spurmodells treten durch zufällige Prozesse wie Vielfachstreuung auch statistische Fehler auf. Wenn z.B. am Punkt B (s. Abb. 4.1) das Teilchen in positive z-Richtung gestreut wird, so werden ab diesem Punkt die Hits nicht mehr zufällig um die gefittete Spur verteilt sein, sondern bevorzugt zu größeren z verschoben. Die Fehler der Abstände der Hits zur gefitteten Spur sind also nicht unabhängig, und somit muß die gesamte Gewichtsmatrix bestimmt werden (vergleiche Kap. 5). Verallgemeinert man die diagonale Matrix unter Berücksichtigung abhängiger Fehler, so erhält man:

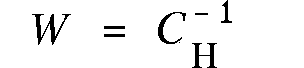(4.12)
C_Hist die Kovarianzmatrix der Hitabstände (s. Kap. 5). Das Gauß-Markov-Theorem sagt aus, daß der in (4.4) benutzte Ansatz für lineare Spurmodelle mit der Lösung (4.11) die besten Spurparameter liefert. Diese Kovarianzmatrix läßt sich auch zur Fehlerberechnung mit Hilfe des Fehlerfortpflanzungsgesetzes benutzen. Für die Kovarianzmatrix C_P der Spurparameter ergibt sich für ein lineares Spurmodell bzw. allgemein in 1. Näherung:

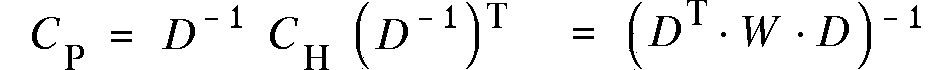(4.13)
Entsprechend lassen sich auch alle sonstigen Fehler von gefitteten Größen berechnen. Dies wird sich später als Vorteil herausstellen, da man so eine weitere Möglichkeit hat, die Gewichtsmatrix zu überprüfen(s. Kap. 5.3).

Weiter zu Kapitel 5
Zum Inhaltsverzeichnis